Answer:
d. 0.3446
Explanation:
We need to calculate the z-score for the given weekly income.
We calculate the z-score of $1000 using the formula

From the question, the standard deviation is
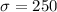 dollars.
dollars.
The average weekly income is
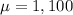 dollars.
dollars.
Let us substitute these values into the formula to obtain:

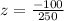

We now read from the standard normal distribution table the area that corresponds to a z-score of -0.4.
From the standard normal distribution table,
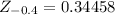 .
.
We round to 4 decimal places to obtain:
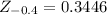 .
.
Therefore the probability that a trainee earns less than $1,000 a week is
 .
.
The correct choice is D.