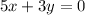Question

A

passes through A(-3,0) and B(-6,5). What is the equation of the line that passes through the origin and is parallel to AB?
OA. 5x - 3y = 0
B. -* + 3y = 0
c. 5x - 3y = 0
D. 3x + 5y = 0
E. -3x + 5y = 0

Answer 1

B. 5x + 3y = 0

Explanation:

Parallel lines have the same slope.

The slope-intercept form of an equation of a line:

`y=mx+b`

m - slope

b - y-intercept

The formula of a slope:

`m=(y_2-y_1)/(x_2-x_1)`

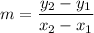
We have the points A(-3, 0) and B(-6, 5). Substitute:

`m=(5-0)/(-6-(-3))=(5)/(-3)=-(5)/(3)`

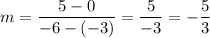
The line passes through the origin, therefore the y-intercept is equal to 0.

Therefore we have the equation:

`y=-(5)/(3)x`

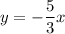
Convert to the standard form
`Ax+By=C`

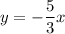`y=-(5)/(3)x` multiply both sides by 3

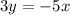`3y=-5x` add 5x to both sides

`5x+3y=0`