Answer:

Explanation:
We are given that an equation
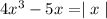
We have to find the solution of given equation and arrange the solution in increasing order.
 when x >0
when x >0
and
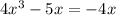 when x < 0
when x < 0
because
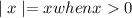
=-x when x < 0
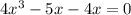
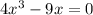


Using identity
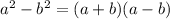
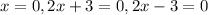
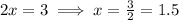

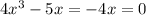
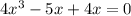
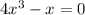
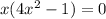
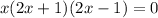
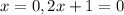
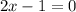
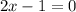

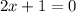
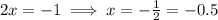
When we substitute x=


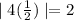
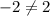
Hence,
 is a not solution of given equation.
is a not solution of given equation.
When substitute
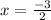

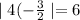
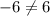
Hence,
 is not a solution of given equation.
is not a solution of given equation.
Substitute x=
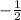 in the given equation
in the given equation


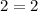
Hence,
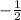 is a solution of given equation.
is a solution of given equation.
Substitute
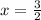 in the given equation
in the given equation

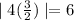
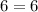
Hence,
 is a solution of given equation.
is a solution of given equation.
Answer:
