Answer:
x=0.76 or -5.26
Explanation:
You can apply the completing square method to solve this ;
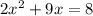
Rewrite the equation with a zero like below
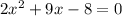
This is by taking 8 to the left side of the equation
Divide the terms by 2 in x²
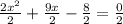
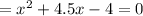
Move the number term to the right side of the equation
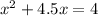
complete square on the lefts side of the equation, how?
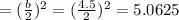
balance the equation by adding this value to the right side , in this form

Factorize the left side
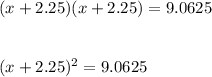
Eliminate the square on the left side
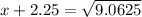
x+2.25= ± 3.010
Solve for x
x=+3.010-2.25=0.76
or
x=-3.010-2.25=-5.26