Answer:
The coefficient of friction is 0.56
Step-by-step explanation:
It is given that,
Mass of the automobile, m = 1400 kg
Speed of the automobile, v = 23 m/s
Radius of the track, r = 95 m
The automobile is moving in a circular track. The centripetal force is given by :
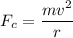 ............(1)
............(1)
Frictional force is given by :
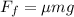 ...................(2)
...................(2)
 = coefficient of friction
= coefficient of friction
g = acceleration due to gravity
From equation (1) and (2), we get :

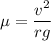
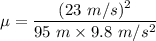
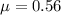
So, the coefficient of friction is 0.56. Hence, this is the required solution.