Answer:
Y = 2/3x - 3
Explanation:
Recall the general equation for a straight line is
y = mx + b
where m is the gradient and b is the y-intercept
given 2 points whose coordinates are (x1, y1) and (x2, y2), m can be found with the following formula:
m =
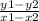
in this case, x1 = 3, y1 = -1, x2 = 6, y2=1
applying these values to the formula for m will give
m = (-1 -1) / (3-6) = 2/3
We can see immediately that only the first (top-most) answer has this value for m and we can guess that this is probably the answer.
But we can still check to confirm:
If we substitute this back into the general equation, we get:
y = (2/3)x + b
In order to find the value for b, we substitute any one of the 2 given points back into this equation. Lets choose (6,1)
1 = (2/3)(6) + b
1 = 4 + b
b = -3
Confirm Y = 2/3x - 3 is the answer.