Answer:
Choice C)
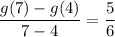 .
.
Explanation:
The average rate of change of a function is:
 .
.
Note that
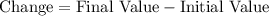 .
.
For this question,
- Initial Independent Variable value: 4;
- Final Independent Variable value: 7.
As a result,
- Change in Independent Variable value:
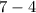 .
.
- Initial function value: g(4);
- Final function value: g(7).
As a result,
- Change in function value:
 .
.
The average rate of change in the value of
 between
between
 and
and
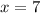 will be:
will be:
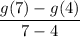 .
.