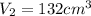Answer:

Step-by-step explanation:
The volume
 of a solid is given by the multiplication of its three dimensions:
of a solid is given by the multiplication of its three dimensions:
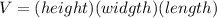
In this case we have two similar solids with volumes
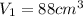 and
and
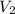 , and we only have information about the height of each solid
, and we only have information about the height of each solid
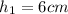 and
and
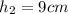 .
.
Now, there is a theorem for similar solids, which establishes the ratio of their volume is
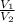 and the ratio of one of their corresponding sides (the height in this case) is
and the ratio of one of their corresponding sides (the height in this case) is
 .
.
Knowing this, we can write the following relation:
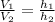
Substituting the known values:
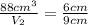
Fially finding
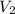 :
: