Question

Which of the following lines is parallel to x = 7? (2 points) a 3y = 7 b y = 7 c x = y d x = 4

Answer 1

Choice d.
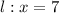`l:x = 7` is parallel to the line
`x = 4`.

Explanation:

Refer to the diagram attached. (Created with GeoGebra)

The line
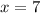`x = 7` is made of all the points on a cartesian plane that meet the requirement
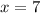`x = 7`. In other words, this line consists of points with x-coordinate
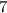`7`. That includes:

• 
  `(7, -1)`,
• 
  `(7,0)`, and
• 
  `(7,1)`.

That line is perpendicular to the x-axis (the horizontal axis) and intersects the x-axis at the point
`(7,0)`.

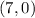Now, consider the lines in the choices.

The first line
`3y =7` requires only that the y-coordinates of its points be 7/3. This line accepts any x-values. Points on this line include:

• 
  `\displaystyle \left(-1, (7)/(3)\right)`,
• 
  `\displaystyle \left(0, (7)/(3)\right)`, and
• 
  `\displaystyle \left(-1, (7)/(3)\right)`.

As a result, this line is parallel to the y-axis and is perpendicular to the line
`x = 7`.

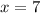Similar to the first, the second line
`y = 7` is also parallel to the y-axis and is perpendicular to the line
`x = 7`.

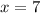The third line
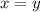`x = y` requires that the x- and y- coordinates of all its points be equal. Points may include:

• 
  `(-1, -1)`,
• 
  `(0,0)`, and
• 
  `(1,1)`.

This line is slant.

The last line
`x = 4` is similar to the given line
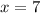`x = 7`. This line is also perpendicular to the x-axis. The difference is that this line is three units to the left of the line
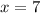`x = 7`.