Question

The surface area of a rectangular prism is increased by a factor of 16.

By what factor is the volume of the figure increased?

Answer 1

The volume of the rectangular prism will increase by a factor of 64.

Explanation:

Surface area =
`length* length`

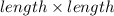
or
`√(surface area) =length`

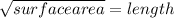
Therefore, the increase in the length of the sides will be =
`√(16)=4`

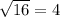
We know the volume is =
`length* width* height`

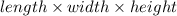
When there is increase in length of sides by 4 times, then volume will increase by
`4^(3)`

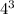
And
`4^(3)` =
`4*4*4=64`

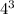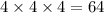
Hence, the volume of the rectangular prism will increase by a factor of 64.

Answer 2

The factor of the volume of the figure increased is 64

Explanation:

we know that

If two figures are similar, then the ratio of its surface areas is equal to the scale factor squared and the ratio of its volumes is equal to the scale factor elevated to the cube

step 1

Find the scale factor

Let

z ----> the scale factor

z²=16

z=4 -----> scale factor

so

z³=4³=64

The factor of the volume of the figure increased is 64