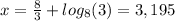2 Answers

Matteo Caprari · Answer 1 · 2020-02-20T11:07:55+0000

Step-by-step answer:

Let's attack the left side:

log_8 12 = log (base 8) 12 = log(12)/log(8) = 1.1949875 (approx.)

Next solve

log_8 12 = x-2

log(12)/log(8) = x-2

x = 2 + log(12)/log(8)

= 3.195 (to one thousandth)

Dale Gerdemann · Answer 2 · 2020-02-24T15:03:10+0000

For this case we have the following expression:

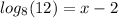
$log_ {8} (12) = x-2$

We rewrite how:

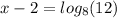
$x-2 = log_ {8} (12)$

We add 2 to both sides of the equation:

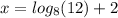
$x = log_ {8} (12) +2$

We rewrite
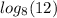$log_ {8} (12)$ as
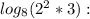
$log_ {8} (2 ^ 2 * 3):$

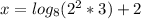
$x = log_ {8} (2 ^ 2 * 3) +2$

We apply logarithm properties:

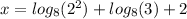
$x = log_ {8} (2 ^ 2) + log_ {8} (3) +2$

We apply logarithm properties:

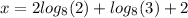
$x = 2log_ {8} (2) + log_ {8} (3) +2$

The logarithmic base 8 of 2 is
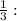
$\frac {1} {3}:$

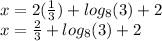
$x = 2 (\frac {1} {3}) + log_ {8} (3) +2\\x = \frac {2} {3} + log_ {8} (3) +2$

We simplify:

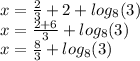
$x = \frac {2} {3} + 2 + log_ {8} (3)\\x = \frac {2 + 6} {3} + log_ {8} (3)\\x = \frac {8} {3} + log_ {8} (3)$

Decimal form:

3,195

Answer:

$x = \frac {8} {3} + log_ {8} (3) = 3,195$

Please log in or register to add a comment.