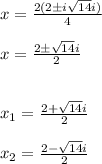Answer:
OPTION E:
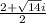
Explanation:
Given the Quadratic equation
 , you can find the roots by applying the Quadratic formula. This is:
, you can find the roots by applying the Quadratic formula. This is:
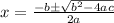
In this case you can identify that:
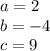
Then you can substitute values into the Quadratic formula:
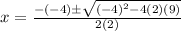
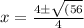
Remember that
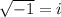 , then:
, then:
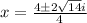
Simplifying, you get: