Question

Factor the Higher degree polynomial

5y^4 + 11y^2 + 2

Answer 1

`\bf 5y^4+11y^2+2\implies 5(y^2)^2+11y^2+2\implies (5y^2+1)(y^2+2)`

Answer 2

For this case we must factor the following polynomial:

`5y ^ 4 + 11y ^ 2 + 2`

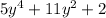
We rewrite
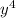`y ^ 4`as
`(y^ 2) ^ 2`:

`5 (y ^ 2) ^ 2 + 11y ^ 2 + 2`

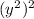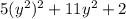
We make a change of variable:

`u = y ^ 2`

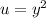
We replace:

`5u ^ + 11u + 2`

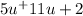
we rewrite the middle term as a sum of two terms whose product of 5 * 2 = 10 and the sum of 11.

So:

`5u ^ 2 + (1 + 10) u + 2`

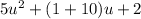
We apply distributive property:

`5u ^ 2 + u + 10u + 2`

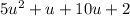
We factor the highest common denominator of each group.

`(5u ^ 2 + u) + (10u + 2)\\u (5u + 1) +2 (5u + 1)`

We factor again:

`(u + 2) (5u + 1)`

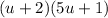
Returning the change:

`(y ^ 2 + 2) (5y ^ 2 + 1)`

ANswer:

`(y ^ 2 + 2) (5y ^ 2 + 1)`