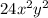Question

In two or more complete sentences, prove how to find the third term of the expansion of (2x + y)4.

Answer 1

The third term is
`24x^2y^2`

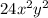
Explanation:

The formula used to find the third term of the expansion (2x+y)^4 is called Binomial Theorem

The Binomial Theorem is:

`(x+a)^n = \sum_(k=0)^(n) {n \choose k}x^ka^(n-k)\\`

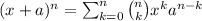
In the given question x = 2x

a = y

n = 4

We have to find the third term, so value of k will be 2 as k starts from 0

Putting the values in the Binomial Theorem

`= {4 \choose 2}(2x)^2(y)^(4-2)\\= {4 \choose 2}4x^2(y)^(2)`

`{n \choose k}==(n!)/(k!(n-k)!)`

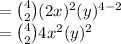
Putting the values:

`= {4 \choose 2}4x^2(y)^(2)\\=(4!)/(2!(4-2)!)4x^2(y)^(2)\\=(4!)/(2!2!)4x^2y^(2)\\=(4*3*2*1)/(2*2)4x^2y^(2)\\=(24)/(4)4x^2y^(2)\\=6*4x^2y^(2)\\=24x^2y^2`

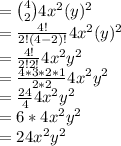
So, the third term is
`24x^2y^2`