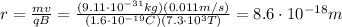Answer:
Step-by-step explanation:
Initially, the electron is travelling undeflected at constant speed- this means that the electric force and the magnetic force acting on the electron are balanced. So we can write
q E = q v B
where
q is the electron's charge
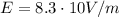 is the electric field magnitude
is the electric field magnitude
v is the electron's speed
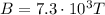 is the magnitude of the magnetic field
is the magnitude of the magnetic field
Solving for v,
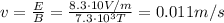
Then the electric field is turned off, so the electron (under the influence of the magnetic field only) will start moving in a circle of radius r. Therefore, the magnetic force will be equal to the centripetal force:
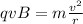
where
 is the electron's charge
is the electron's charge
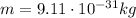 is the electron's mass
is the electron's mass
Solving for r, we find the radius of the electron's orbit: