Question

The graph of y = ax 2 + bx + c is a parabola that opens up and has a vertex at (-2, 5). What is the solution set of the related equation 0 = ax 2 + bx + c?

Answer 1

`y=(-5)/(4)x^(2) -5b`

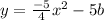
Explanation:

Assume c = 0

Using the formula for the x-coordinate of the vertex, b can be calculated in terms of a:

`x=(-b)/(2a) \\-2=(-b)/(2a) \\b=4a`

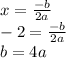
B can then be substituted into the quadratic equation, along with the coordinates of the vertex, to solve a:

`y=ax^(2)+bx\\y=ax^(2)+4ax\\5=a(-2)^(2)+4(-2)a\\5=4a-8a\\5=-4a\\a=(5)/(-4)`

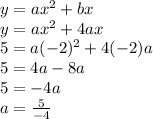
AND

`b=4a\\b=(-5)/(4) *4\\b=-5`

Substituting into the quadratic equation:

`y=(-5)/(4)x^(2) -5b`

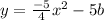
Because a is negative, the parabola opens up.

Answer 2

The solution set is ∅

Explanation:

The expression

y = ax^2 + bx + c

is a quadratic equation.

The vertex is located at (-2, 5) and the graph opens up, this means that it never intercepts the x-axis.

The solution set is ∅

Please see attached image