Question

The graph of y = ax 2 + bx + c is a parabola that opens up and has a vertex at (-2, 5). What is the solution set of the related equation 0 = ax 2 + bx + c?

Answer 1

The answer is impossible so is Ф

Answer 2

I have provided two solutions both concluding the same thing.

There is no solution.

Simplest solution says this is a parabola opened up at vertex (-2,5) which means it never crosses the x-axis. There is no solution because thee curve does not touch the x-axis.

Explanation:

Harder solution (algebraic solution):

The vertex form a parabola is
`y=a(x-h)^2+k`

We are given the vertex (h,k) is (-2,5)

So we have
`y=a(x+2)^2+5`

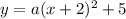
Now we also know
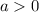`a>0` since the parabola opens up.

That is all we know about a.

Let's see what
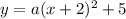`y=a(x+2)^2+5` is in standard form

`y=a(x+2)(x+2)+5\\y=a(x^2+4x+4)+5\\y=ax^2+4ax+4a+5\\\\`

So we are asked to solve for the solution set of

`0=ax^2+4ax+4a+5\\A=a\\B=4a\\C=4a+5\\\\`

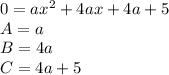
Plug into quadratic formula

I'm going to write the quadratic formula with the capital letters to be less confusing:

`x=(-B \pm √(B^2-4AC))/(2A)\\x=(-4a \pm √(16a^2-4(a)(4a+5)))/(2a)\\x=(-4a \pm √(16a^2-16a^2-20a))/(2a)\\x=(-4a \pm √(-20a))/(2a)\\x=(-4a \pm √(4) √(-5a))/(2a)\\x=(-4a \pm 2 √(-5a))/(2a)\\x=(-4a)/(2a) \pm (√(-5a))/(a)\\`

This says
`a` has to be negative... The inside of the square root... So there was no real solution.\\

\\

Simpler solution (graph/visual)

You could have also drawn a parabola open up with vertex at (-2,5) and we should have seen that it was impossible it cross the x-axis.