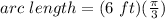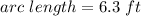Question

how long is the arc intersected by a central angle of π/3 radians in a circle with a radius of 6 feet round your answer to the nearest tenth

Answer 1

`\bf \textit{arc's length}\\\\ s=r\theta ~~ \begin{cases} r=radius\\ \theta =angle~in\\ \qquad radians\\ \cline{1-1} r=6\\ \theta =(\pi )/(3) \end{cases}\implies s=6\left( (\pi )/(3) \right)\implies s=2\pi \implies \stackrel{\textit{rounded up}}{s=6.3}`

Answer 2

Answer:
`arc\ length=6.3\ ft`

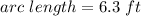
Explanation:

You need to use the following formula for calculate the arc lenght:

`arc\ length=r\theta`

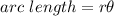
Where "r" is the radius and
`\theta` is the central angle in radians.

You know that the central angle in radians s:

`\theta=(\pi )/(3)`

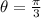
And the radius is:

`r=6\ ft`

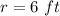
Therefore, the final step is to substitute the values into the formula. Then you get:

`arc\ length=(6\ ft)((\pi )/(3))`

`arc\ length=6.3\ ft`