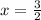Question

how do you find the equation of the axis of symmetry and the coordinates of the vertex of the graph of the function y= -2x^2+6x-1

Answer 1

The vertex is:
`((3)/(2),\ (7)/(2))`

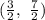
The axis of symmetry is:

`x=(3)/(2)`

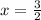
Explanation:

For a quadratic equation of the form:

`y=ax^2 + bx +c`

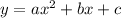
The vertex of the parabola will be the point:
`(-(b)/(2a),\ f(-(b)/(2a)))`

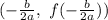
In this case we have the following equation:

`y= -2x^2+6x-1`

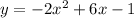
Note that:

`a=-2\\b=6\\c=-1`

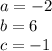
Then the x coordinate of the vertex is:

`x=-(b)/(2a)`

`x=-(6)/(2(-2))`

`x=(3)/(2)`

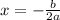
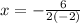
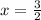
Then the y coordinate of the vertex is:

`y= -2((3)/(2))^2+6((3)/(2))-1`

`y=(7)/(2)`

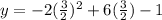
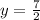
The vertex is:
`((3)/(2),\ (7)/(2))`

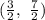
For a quadratic function the axis of symmetry is always a vertical line that passes through the vertex of the function.

Then the axis of symmetry is:

`x=(3)/(2)`