Answer: Option D
g(x) is shifted 3 units to the left and reflected over the x-axis.
Explanation:
If we have a function f(x) and make a transformation of the form:

Then it is true that:
If
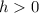 the graph of g(x) is equal to the graph of f(x) displaced h units to the left
the graph of g(x) is equal to the graph of f(x) displaced h units to the left
If
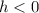 the graph of g(x) is equal to the graph of f(x) displaced h units to the right
the graph of g(x) is equal to the graph of f(x) displaced h units to the right
Also if we have a function f(x) and perform a transformation of the form:

Then it is true that:
The graph of g(x) is equal to the graph of f(x) reflected on the x axis.
In this case
 and
and
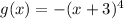
So
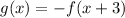
Then
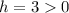 . Therefore the graph of g(x) is equal to the graph of f(x) displaced 3 units to the left and reflected on the x axis
. Therefore the graph of g(x) is equal to the graph of f(x) displaced 3 units to the left and reflected on the x axis
The answer is the option D