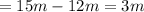Question

A force of 60 N is used to stretch two springs that are initially the same length. Spring A has a spring constant of 4 N/m, and spring B has a spring constant of 5 N/m.

How do the lengths of the springs compare?

A:Spring B is 1 m longer than spring A because 5 – 4 = 1.
B:Spring A is the same length as spring B because 60 – 60 = 0.
C:Spring B is 60 m longer than spring A because 300 – 240 = 60.
D:Spring A is 3 m longer than spring B because 15 – 12 = 3.

Answer 1

D)Spring A is 3 m longer than spring B because 15 – 12 = 3.

trust

Answer 2

D:Spring A is 3 m longer than spring B because 15 – 12 = 3.

Explanation:

In this question, you should remember the Hooke's Law in physics.

The Hooke's Law simply explains that the extension that occurs on a spring is directly proportional to the load applied on it.

The mathematical expression for this law is

`F=-kx`

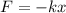
where;

F= force applied on the spring

x = the extension on the spring

k= the spring constant which varies in spring.

The question will need you to calculate the extension on the springs A and B then compare the values obtained.

In spring A

Force, F=60N and spring constant ,k=4 N/m

To find the extension x apply the expression;

`F=-kx\\\\60=-4*x\\\\60=-4x\\\\(60)/(-4) =(-4x)/(-4) \\\\\\-15=x`

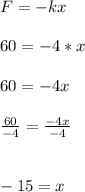
Here the spring extension is 15 m

In spring B

Force, F=60N and spring constant , k=5N/m

To find the extension x apply the same expression

`F=-kx\\\\60=-5*x\\\\60=-5x\\\\\\(60)/(-5) =(-5x)/(-5) \\\\\\-12=x`

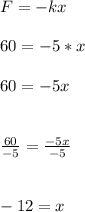
Here the extension on the spring is 12 m

Compare

The extension on spring A is 3 m longer than that in spring B because when you subtract the value of spring B from that in spring A you get 3m

`=15m-12m=3m`