Question

Find the vertices and foci of the hyperbola with equation quantity x plus one squared divided by sixteen minus the quantity of y plus five squared divided by nine = 1.

A. Vertices: (-5, 3), (-5, -5); Foci: (-5, -6), (-5, 4)

B. Vertices: (2, -5), (-4, -5); Foci: (-4, -5), (2, -5)

C. Vertices: (3, -5), (-5, -5); Foci: (-6, -5), (4, -5)

D. Vertices: (-5, 2), (-5, -4); Foci: (-5, -4), (-5, 2)

Answer 1

C

Explanation:

This hyperbola is a horizontal hyperbola of the standard form:

`((x-h)^2)/(a^2)-((y-k)^2)/(b^2)=1`

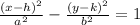
Since our equation is

`((x+1)^2)/(16)-((y+5)^2)/(9)=1`,

a = 4 and b = 3.

The coordinates for the vertices are (±a, 0) and

the coordinates for the foci are (±c, 0).

We have a, but we need c. To find c, we use Pythagorean's Theorem:

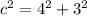`c^2=4^2+3^2` or

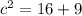`c^2=16+9` giving us that

c = 5.

But these a and c values have to be figured from the center of the hyperbola which is located at (-1, -5).

For the vertices, then, we add the a value of 4 and -4 to the x value of the center, which is -1. The -5 remains, since the vertices and the foci are on the same transcersal axis which is the line y = -5.

For the foci, then, we add the c value of 5 to -1, and again the -5 remains in the y position.

Vertices: (-1+4, -5)-->(3, -5) and (-1-4, -5)-->(-5, -5)

Foci: (-1+5, -5)-->(4, -5) and (-1-5, -5)-->(-6, -5)

Choice C