Question

A bottling company uses a filling machine to fill plastic bottles with popular cola. The contents are known to vary according to a normal distribution with mean μ = 300 ml and standard deviation σ = 10 ml. What is the probability that the mean contents of the bottles in a six pack is less than 295 ml?

Answer 1

Answer: 0.3085

Explanation:

Given: Mean :
`\mu=300\text{ ml}`

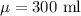
Standard deviation :
`\sigma=10\text{ ml}`

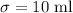
The formula to calculate the value of z-score :-

`z=(X-\mu)/(\sigma)`

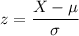
For X = 295 ml, we have

`z=(295-300)/(10)=-0.5`

The p-value of z =
`P(Z=z<-0.5)=0.3085`

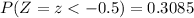
Hence, the probability that the mean contents of the bottles in a six pack is less than 295 ml =0.3085