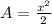For this case we have that by definition, if we draw the diagonal of a square two rectangular triangles are formed. If the diagonal measures "x", then the Pythagorean theorem is fulfilled:
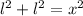
Where:
l: It's the side of the square.
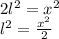
We know that the area of a square is given by:
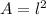
So, the area is:
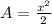
Answer: