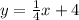Question

Which of the following equations represents a line that is perpendicular to

y = -4x+9 and passes through the point, (4, 5)?
A. y- x+5 B. y- *x+6
C. y = x+4 D. y --4x+4

Answer 1

For this case we have that if two lines are perpendicular, then the product of their slopes is -1.

If we have the following equation of the line:

`y = -4x + 9`

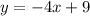
The slope is
`m_ {1} = - 4`

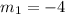
Then yes:

`m_ {1} * m_ {2} = - 1\\m_ {2} = \frac {-1} {m_ {1}}\\m_ {2} = \frac {-1} {- 4}\\m_ {2} = \frac {1} {4}`

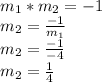
The equation of the new line will be:

`y = \frac {1} {4} x + b`

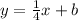
We substitute the point to find "b":

`5 = \frac {1} {4} (4) + b\\5 = 1 + b\\b = 5-1\\b = 4`

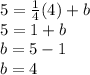
Finally, the equation is:

`y = \frac {1} {4} x + 4`

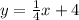
Answer:

`y = \frac {1} {4} x + 4`