Question

Part A: Sam rented a boat at $225 for 2 days. If he rents the same boat for 5 days, he has to pay a total rent of $480.

Write an equation in the standard form to represent the total rent (y) that Sam has to pay for renting the boat for x days. (4 points)

Part B: Write the equation obtained in Part A using function notation.(2 points)

Part C: Describe the steps to graph the equation obtained above on the coordinate axes. Mention the labels on the axes and the intervals. (4 points)

Answer 1

Here's what I get.

Explanation:

Part A. Equation in standard form

The question is asking you to find the equation of a straight line that passes through two points

Let x = the number of days

and y = the cost

Then the coordinates of the two points are (2,225) and (5,480).

(i) Calculate the slope of the line

`\begin{array}{rcl}m & = & (y_(2) - y_(1))/(x_(2) - x_(1))\\\\& = & (480 - 225)/(5 - 2)\\\\& = & (255)/(3)\\\\& = & 85\\\end{array}`

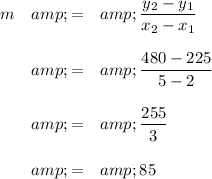
In other words, the daily rental is $85/day.

(ii) Calculate the y-intercept

`\begin{array}{rcl}y & = & mx + b\\480 & = & 85 * 5 + b\\480 & = & 425 + b\\b & = & 55\\\end{array}`

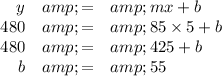
(iii) Write the equation for the line

y = 85x + 55

That is, the cost is $55 plus $85/day

Part B. Equation in function notation

Replace y with ƒ(x)

ƒ(x) = 85x + 55

Part C. Graphing

Let's say you want to plot a graph of the rental cost for up to ten days.

(i) Calculate two points on the graph.

When x = 0, y = 85; when x = 10, y = 905.

(ii) Scale your axes

A good number of intervals is about ten.

Your x-axis should have tick marks at 1-day intervals.

Your largest y-value is 905. Ten intervals would make about $90/interval. However, you should round that up to $100/interval for easy interpolation.

Your y-axis will run from 0 to $1000 in $100 intervals.

Plot your two points and draw a straight line through them.

(iii) Axis labels

x represents the number of days, so the label on the x-axis could be "No. of days."

y represents the cost of renting the boat, so the label on the y-axis could be "Rental cost."

Your graph should resemble the one below.