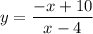Question

Which system of equations is represented by the graph?

A) y = x
y = -x-10, over x-4

B) y = −x
y = x+10, over x-4

C) y = x
y = -x+10 divided by the quantity x-4

D) y = −x
y = -x+10 divided by the quantity x-4

Answer 1

`\large\boxed{C)\ \left\{\begin{array}{ccc}y=x\\\\y=(-x+10)/(x-4)\end{array}\right}`

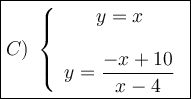
Explanation:

We have the points

(-2 , -2) → x = -2 and y = -2 → x = y

(5, 5) → x = 5 and y = 5 → x = y

The equation of a line is
`y=x`

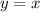
The hyperbola has the vertical asymptote x = a and the horizontal asymptote y = -1.

Therefore the second equation is:

`y=(a)/(x-4)-1=(a)/(x-4)-(x-4)/(x-4)=(a-(x-4))/(x-4)=(a-x+4)/(x-4)`

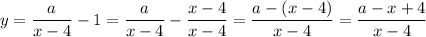
Where a > 0.

The corresponding equation in the solutions to choose is:

`y=(-x+10)/(x-4)`