Question

A collegiate video-game competition team has a 0.70 probability of winning a match. Over the course of a season, 8 matches are played. Individual matches are independent of any other matches. Calculate the probability that the team will win exactly 7 matches over the course of one season.

Answer 1

The probability that the team will win exactly 7 matches over the course of one season is:

0.1977

Explanation:

We know that the probability of k successes out of n successes is given by the binomial distribution as:

`P(X=k)=n_C_kp^k(1-p)^(n-k)`

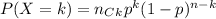
where p is the probability of success .

Here we are asked to find the probability that the team will win exactly 7 matches over the course of one season.

Since, there are 8 matches over the course of season.

This means n=8

and k=7

and p=0.70

(Since, 0.70 probability of winning a match )

Hence, we get:

`P(X=7)=8_C_7* (0.70)^7* (1-0.70)^(8-7)\\\\i.e.\\\\P(X=7)=8* (0.70)^7* 0.30\\\\i.e.\\\\P(X=7)=0.1977`

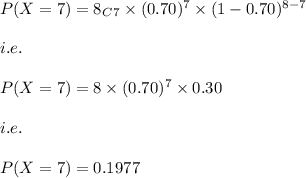
Hence, the answer is:

0.1977