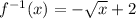Answer:
Look to the bold answer down
Explanation:
* Lets explain how to restrict the domain of the quadratic function
- The quadratic function is two-to-one function
- The inverse of it is one-to-two which is not a function
- So we can not find the inverse of the quadratic function until restrict its
domain
- We restrict the domain at the x-coordinate of the vertex of the function
∵ f(x) = (x - h)² + k is the standard form of the quadratic function, where
(h , k) are the coordinates of its vertex
- To restrict the domain we put x > h for the right part of the parabola
or x < h for the left part of the parabola
* Lets solve the problem
∵ f(x) = (x - 2)²
∵ f(x) = (x - h)² + k is the standard form of the quadratic function
∴ h = 2 and k = 0
∴ The vertex of the parabola is (2 , 0)
- We will restrict the domain at x = 2
∴ The domain of the function f(x) to have inverse is x > 2 or x < 2
* The restriction domain is x > 2 or x < 2
- To find the inverse of the function switch x and y and solve for the
new y
∵ f(x) = (x - 2)²
∵ f(x) = y
∴ y = (x - 2)²
- Switch x and y
∴ x = (y - 2)²
- take square root for both sides
∴ ± √x = y - 2
- Add 2 for both sides
∴ ± √x + 2 = y
∴

* For the domain x > 2 of f(x) the inverse is
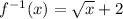
For the domain x < 2 of f(x) the inverse is