Question

Taylor fires a toy rocket from ground level. The height of the rocket with respect to time can be represented by quadratic function. If the toy rocket reaches a maximum height of 34 feet, 3 seconds after it was fired, which of the following functions could represent the height, h, of the rocket t seconds after it was fired?

A) h(t)=-16(t-3)²+34

B) h(t)=-16(t+3)²+34

C) h(t)=16(t-3)²+34

D) h(t)=16(t+3)²+34

Answer 1

The function in choice

A)
`h(t) = -16(t - 3)^(2) + 34`

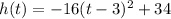
could possibly represent this relationship.

Explanation:

Consider the vertex form of parabolas with a local extrema at
`(x_(0), y_(0))`.

`y = a(x - x_(0))^(2) + y_0`.

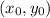Note the minus sign in front of
`x_0` in this expression.

The coefficient
`a` cannot be zero. The value of
`a` depends on the direction and width of the parabola's opening:

• 
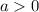  `a > 0` if the parabola opens upwards, and
• 
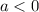  `a < 0` if the parabola opens downwards.
• The width of the opening decreases as the value of
  `a` increases.

For this parabola,

• 
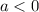  `a < 0` since the parabola opens downwards: the height of the rocket will eventually decrease as the rocket falls back to the ground;
• 
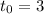  `t_0 = 3`, and
• 
  `h_0 = 34`.

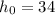Among the four functions, only the function in A) meets the requirements.