Answer:
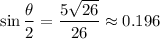 .
.
Explanation:
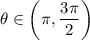 ,
,
such that
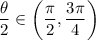 .
.
As a result,
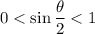 , and
, and
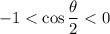 .
.
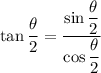 ,
,
such that
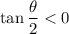 .
.
Let
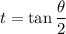 .
.
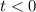 .
.
By the double angle identity for tangents.
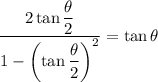 .
.
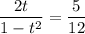 .
.
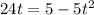 .
.
Solve this quadratic equation for
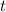 :
:
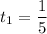 , and
, and
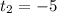 .
.
Discard
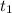 for it is not smaller than zero.
for it is not smaller than zero.
Let
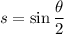 .
.
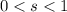 .
.
By the definition of tangents:
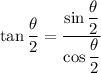 .
.
Apply the Pythagorean Algorithm to express the cosine of
 in terms of
in terms of
 . Note that
. Note that
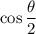 is expected to be smaller than zero.
is expected to be smaller than zero.
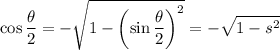 .
.
Solve for
 :
:
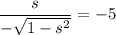 .
.
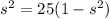 .
.
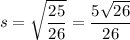 .
.
Therefore
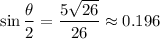 .
.