Question

12. Meldre put $5000 in a savings account that pays 1.25% interest compounded yearly. How much money will be in the account 10 years later if she makes no more deposits or withdrawals?

Answer 1

Answer: $5,661.35

Explanation:

I used the exponential growth formula to get my answer.

Answer 2

We know that, Final Amount in Compound Interest is given by :

`\bigstar\;\;\boxed{\mathsf{Amount = Principal\left(1 + (Rate\;of\;interest)/(100)\right)^(Number\;of\;Years)}}`

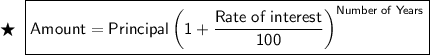
Given :

● Principal = $5000

● Rate of interest = 1.25

● Number of Years = 10

Substituting the values in the Formula, We get :

`\implies \mathsf{Amount = 5000\left(1 + (1.25)/(100)\right)^(10)}`

`\implies \mathsf{Amount = 5000\left(1 + (0.25)/(20)\right)^(10)}`

`\implies \mathsf{Amount = 5000\left(1 + (0.05)/(4)\right)^(10)}`

`\implies \mathsf{Amount = 5000\left((4.05)/(4)\right)^(10)}`

`\implies \mathsf{Amount = 5000* (1.0125)^(10)}`

`\implies \mathsf{Amount = 5661.354}`

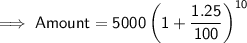
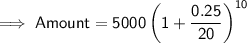
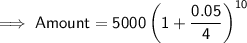
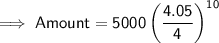
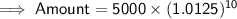
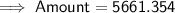
Answer : $5661.354 money will be in the account 10 years later