Answer:
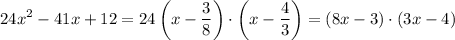 .
.
Explanation:
Apply the quadratic formula to find all factors. For a quadratic equation in the form
 ,
,
where
 ,
,
 , and
, and
 are constants, the two roots will be
are constants, the two roots will be
 , and
, and
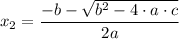 .
.
For this quadratic polynomial,
Apply the quadratic formula to find any
 value or values that will set this polynomial to zero:
value or values that will set this polynomial to zero:
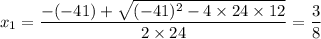 .
.
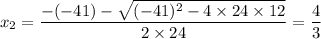 .
.
Apply the factor theorem to find the two factors of this polynomial:
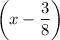 for the root
for the root
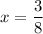 , and
, and
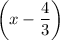 for the root
for the root
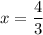 .
.
Keep in mind that simply multiplying the two factors will not reproduce the original polynomial. Doing so assumes that the leading coefficient of
 in the original polynomial is one, which isn't the case for this question.
in the original polynomial is one, which isn't the case for this question.
Multiply the product of the two factors by the leading coefficient of
 in the original polynomial.
in the original polynomial.
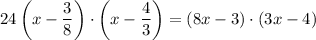 .
.
Expand to make sure that the factored form is equivalent to the original polynomial:
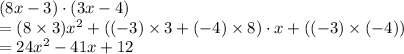 .
.