Answer:
The volume of this pyramid is 16 cm³.
Explanation:
The volume
 of a solid pyramid can be given as:
of a solid pyramid can be given as:
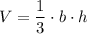 ,
,
where
 is the area of the base of the pyramid, and
is the area of the base of the pyramid, and
 is the height of the pyramid.
is the height of the pyramid.
Here's how to solve this problem with calculus without using the previous formula.
Imaging cutting the square-base pyramid in half, horizontally. Each horizontal cross-section will be a square. The lengths of these squares' sides range from 0 cm to 3 cm. This length will be also be proportional to the vertical distance from the vertice of the pyramid.
Refer to the sketch attached. Let the vertical distance from the vertice be
 cm.
cm.
- At the vertice of this pyramid,
 and the length of a side of the square is also
and the length of a side of the square is also
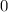 .
. - At the base of this pyramid,
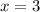 and the length of a side of the square is
and the length of a side of the square is
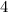 cm.
cm.
As a result, the length of a side of the square will be
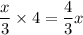 .
.
The area of the square will be
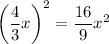 .
.
Integrate the area of the horizontal cross-section with respect to

- from the top of the pyramid, where
 ,
, - to the base, where
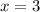 .
.
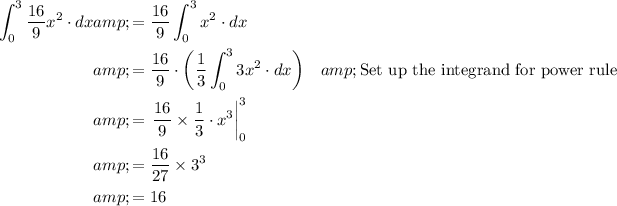 .
.
In other words, the volume of this pyramid is 16 cubic centimeters.