Question

What is the range of the following function:
y = 2(5^x) - 1

Answer 1

Hello!

The answer is:

The range of the function is:

Range: y>2

or

Range: (2,∞+)

Why?

To calculate the range of the following function (exponential function) we need to perform the following steps:

First: Find the value of "x"

So, finding "x" we have:

`y=2(5^(x)-1)\\(y)/(2)=5^(x)-1\\\\(y)/(2)-1=5^(x)\\\\Log_(5)((y)/(2)-1)=Log_5(5^(x))\\\\x=Log_(5)((y)/(2)-1)`

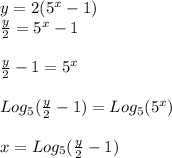
Second: Interpret the restriction of the function:

Since we are working with logarithms, we know that the only restriction that we found is that the logarithmic functions exist only from 0 to the possitive infinite without considering the number 1.

So, we can see that if the variable "x" is a real number, "y" must be greater than 2 because if it's equal to 2 the expression inside the logarithm will tend to 0, and since the logarithm of 0 does not exist in the real numbers, the variable "x" would not be equal to a real number.

Hence, the range of the function is:

Range: y>2

or

Range: (2,∞+)

Note: I have attached a picture (the graph of the function) for better understanding.

Have a nice day!