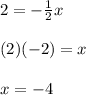Question

A line has a slope of -1 over two and a Y intercept of -2 what is the X intercept of the line

Answer 1

Answer:
`x=-4`

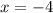
Explanation:

The equation of the line in Slope-Intercept form is:

`y=mx+b`

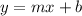
Where "m" is the slope of the line and "b" is the y-intercept.

We know that the slope of this line is:

`m=-(1)/(2)`

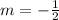
And the y-intercept is:

`b=-2`

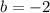
Since the line intersects the x-axis when
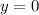`y=0`, we can substitute values into
`y=mx+b`:

`0=-(1)/(2)x-2`

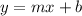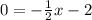
The final step is to solve for "x", then:

`2=-(1)/(2)x\\\\(2)(-2)=x\\\\x=-4`