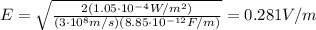(a) 2.97 m
The wavelength of an electromagnetic wave is given by:
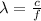
where
 is the wavelength
is the wavelength
c is the speed of light
f is the frequency
For the radio wave in the problem, the frequency is
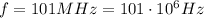
Therefore, the wavelength is
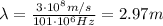
(b)

The intensity of the radio signal is given by

where
P is the power of the signal
A is the area over which the signal is radiated
In this situation:
P = 50,000 W is the power
the area is a hemisphere with a radius of
r = 8.70 km = 8700 m
So the area to be considered is
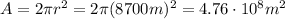
Therefore, the intensity of the signal is

(c) 0.281 V/m
The intensity of an electromagnetic wave can be written as
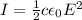
where
c is the speed of light
 is the vacuum permittivity
is the vacuum permittivity
E is the amplitude of the electric field
Re-arranging the equation, we get
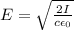
And substituting
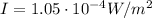
we find