Hello!
The answer is:
The velocity with which the ball can be thrown to have a maximum range of 20 meters is equal to 14 m/s.
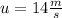
Why?
To solve the problem and find the velocity, we need to isolate it from the equation used to calculate the maximum horizontal range.
We have the equation:
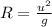
Where,
R is the maximum horizontal range.
u is the initial velocity.
g is the gravity acceleration.
Also, from the statement we know that:

So, using the given information, and isolating, we have:
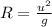
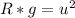

Hence, we have that the velocity with which the ball can be thrown to have a maximum range of 20 meters is equal to 14 m/s.
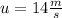
Have a nice day!