Answer:
1) You find the solution by identifying the x-intercepts.
2) Possible real solutions:
- One real solution.
- Two distinct real solutions.
Explanation:
1) The graph of a quadratic equation is a parabola.
By definition, the x-intercepts (Where
 ) are the solutions of the quadratic equation .
) are the solutions of the quadratic equation .
2) Given a quadratic equation
 , you can know the number of real solutions by using this formula to find the Discriminant :
, you can know the number of real solutions by using this formula to find the Discriminant :

If
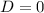 , then there is one real solution with multiplicity two.
, then there is one real solution with multiplicity two.
If
 , then there are two distinct real solutions.
, then there are two distinct real solutions.
On a graph:
-If the graph has two x-intercepts, then the quadratic equation has two real solutions.
-If the graph has one x-intercept , then the quadratic equation has one real solution.