Not entirely sure what the question is supposed to say, so here's my best guess.
First, find the partial fraction decomposition of
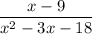
This is equal to
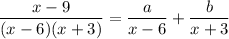
Multiply both sides by
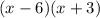 , so that
, so that
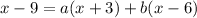
Notice that if
 , the term involving
, the term involving
 vanishes, so that
vanishes, so that
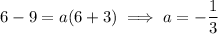
Then if
 , the term with
, the term with
 vanishes and we get
vanishes and we get
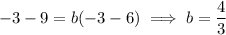
So we have
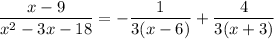
I think the final answer is supposed to be
 , so you end up with 1.
, so you end up with 1.