Question

Calculus 2: I need help with u substitution and intergration by parts. Can someone help me understand the concept?​

Answer 1

Computing an integral by substitution is the reverse of the chain rule for computing the derivative. Substitution is intended to rewrite a complicated-looking integral involving the derivative of some component expression as another much simpler integral. For example, if
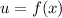`u=f(x)`, then
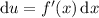`\mathrm du=f'(x)\,\mathrm dx` and

`\displaystyle\int f(x)f'(x)\,\mathrm dx=\int u\,\mathrm du`

###

Integration by parts is the reverse of the product rule for derivatives:

`(f(x)g(x))'=f'(x)g(x)+f(x)g'(x)\implies f(x)g'(x)=(f(x)g(x))'-f'(x)g(x)`

Integrating both sides with respect to
`x` gives

`\displaystyle\int f(x)g'(x)\,\mathrm dx=\int(f(x)g(x))'\,\mathrm dx-\int f'(x)g(x)\,\mathrm dx`

`\displaystyle\int f(x)g'(x)\,\mathrm dx=f(x)g(x)-\int f'(x)g(x)\,\mathrm dx`

###

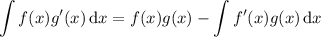
Personally, I think the best way to grasp the idea behind the two methods is to practice. You start to notice patterns to the point where knowing which is the "right" method to use becomes second nature.