Question

Law of cosines: a2 = b2 + c2 – 2bccos(A) Find the measure of J, the smallest angle in a triangle with sides measuring 11, 13, and 19. Round to the nearest whole degree. 30° 34° 42° 47°

Answer 1

The smallest angle occurs opposite the shortest side length of the triangle. So by the law of cosines we have

`11^2=13^3+19^2-2\cdot13\cdot19\cos\angle J\implies\cos\angle J=(409)/(494)\implies\theta\approx\boxed{34^\circ}`

Answer 2

The measure of angle J is 34°

Explanation:

Given,

J is the smallest angle in the triangle with sides measuring 11, 13, and 19,

Thus, J must be the opposite angle of the side measuring 11,

Since, the law of cosines,

`a^2 = b^2 + c^2 - 2bc cos A`

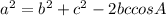
Where, a, b and c are the sides of a triangle ABC,

Such that angle A is opposite to the side measuring a,

By applying the law,

We can write,

`11^2 = 13^2 + 19^2 - 2* 13* 19 cos J`

`121 = 169 + 361 - 494 cos J`

`\implies cos J = (169+361-121)/(494)=(409)/(494)`

`\implies m\angle J=34.1127839945\approx 34^(\circ)`

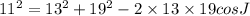
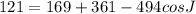
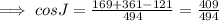
Second option is correct.