Question

The equilibrium constant, Kc, for the following reaction is 1.29×10-2 at 600 K. COCl2(g) CO(g) + Cl2(g) Calculate the equilibrium concentrations of reactant and products when 0.323 moles of COCl2(g) are introduced into a 1.00 L vessel at 600 K.

Answer 1

Answer : The equilibrium concentrations of
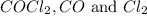`COCl_2,CO\text{ and }Cl_2` are, 0.2646, 0.0584 and 0.0584.

Explanation : Given,

Moles of
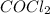`COCl_2` = 0.323 mole

Volume of solution = 1 L

Initial concentration of
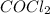`COCl_2` = 0.323 M

Let the moles of
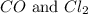`CO\text{ and }Cl_2` be, 'x'. So,

Concentration of
`CO` = x M

Concentration of
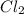`Cl_2` = x M

The given balanced equilibrium reaction is,

`COCl_2(g)\rightleftharpoons CO(g)+Cl_2(g)`

Initial conc. 0.323 M 0 0

At eqm. conc. (0.323-x) M (x M) (x M)

The expression for equilibrium constant for this reaction will be,

`K_c=([CO][Cl_2])/([COCl_2])`

Now put all the given values in this expression, we get :

`1.29* 10^(-2)=((x)* (x))/((0.323-x))`

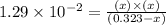
By solving the term 'x', we get :

x = 0.0584

Thus, the concentrations of
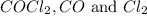`COCl_2,CO\text{ and }Cl_2` at equilibrium are :

Concentration of
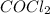`COCl_2` = (0.323-x) M = (0.323-0.0584) M = 0.2646 M

Concentration of
`CO` = x M = 0.0584 M

Concentration of
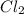`Cl_2` = x M = 0.0584 M

Therefore, the equilibrium concentrations of
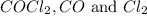`COCl_2,CO\text{ and }Cl_2` are, 0.2646, 0.0584 and 0.0584.