Answer: 0.5237
Explanation:
Mean :
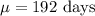
Standard deviation :
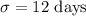
The formula to calculate the z-score is given by :-

For x = 188 days ,
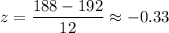
For x = 107 miles per day ,
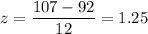
The P-value =
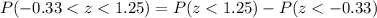
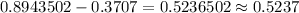
Hence, The probability that a randomly selected pregnancy lasts less than 188 days is approximately 0.5237.