Question

Suppose the lengths of the pregnancies of a certain animal are approximately normally distributed with mean mu equals 192 daysμ=192 days and standard deviation sigma equals 12 daysσ=12 days.What is the probability that a randomly selected pregnancy lasts less than 188188 ​days? The probability that a randomly selected pregnancy lasts less than 188188 days is approximately

Answer 1

Answer: 0.5237

Explanation:

Mean :
`\mu=192\text{ days}`

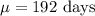
Standard deviation :
`\sigma = 12\text{ days}`

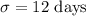
The formula to calculate the z-score is given by :-

`z=(x-\mu)/(\sigma)`

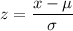
For x = 188 ​days ,

`z=(188-192)/(12)\approx-0.33`

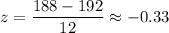
For x = 107 miles per day ,

`z=(107-92)/(12)=1.25`

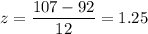
The P-value =
`P(-0.33<z<1.25)=P(z<1.25)-P(z<-0.33)`

`0.8943502-0.3707=0.5236502\approx0.5237`

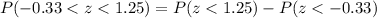
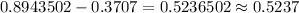
Hence, The probability that a randomly selected pregnancy lasts less than 188 days is approximately 0.5237.