Answer:
The minimum value of the width is 15 ft and the maximum value of the width is 30 ft
Explanation:
Let
x -----> the length of the deck
y ----> the width of the deck
we know that
The perimeter of the deck is equal to
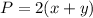
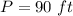
so
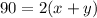
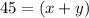
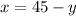 -----> equation A
-----> equation A
The area is equal to
 -----> inequality B
-----> inequality B
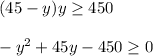
Solve the quadratic equation by graphing
The possible width of the deck are the values of y in the interval
[15,30]
All real numbers greater than or equal to 15 ft and less than or equal to 30 ft
see the attached figure
The minimum value of the width is 15 ft and the maximum value of the width is 30 ft