Answer:
15.7 years
Explanation:
we know that
The deforestation is a exponential function of the form
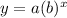
where
y ----> the number of trees still remaining in the forest
x ----> the number of years
a is the initial value (a=500,000 threes)
b is the base
b=100%-4.7%=95.3%=95.3/100=0.953
substitute
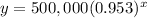
The linear equation of planting threes in the region is equal to
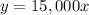
using a graphing tool
Solve the system of equations
The intersection point is (15.7,235,110)
see the attached figure
therefore
For x=15.7 years
The number of trees they have planted will be equal to the number of trees still remaining in the forest