Answer:
Last option
Explanation:
Given expression is:
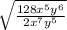
The terms can be simplified one by one
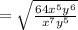
As the larger power of x is in numerator, the smaller power will be brought to denominator
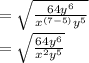
Similarly for y,

Applying the radical
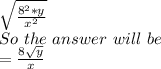
So, last option is the correct answer ..