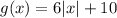Answer: Option A.
Explanation:
There are some transformations for a function f(x).
One of the transformations is:
If
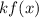 and
and
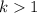 , then the function is stretched vertically by a factor of "k".
, then the function is stretched vertically by a factor of "k".
Therefore, if the function provided
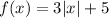 is vertically stretched by a factor or 2, then the transformation is the following:
is vertically stretched by a factor or 2, then the transformation is the following:
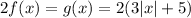
Applying Disitributive property to simplify, we get that the function g(x) is: