Question

1. If the domain of a function f(x) is the set {10, 20, 30}. What does the information tell you about f-1(x)?

2. If the graph of a function f(x) includes the point (3, 0), what point must the graph of f-1(x) include? Explain.


3.The first term in an arithmetic sequence is 2. The twelfth term is 211. Find the value of n so that an = 135.

Answer 1

PART A (1 in diagram)

Each mapping diagram represents a function because none of the elements in the inputs maps on to two different elements in the outputs.

1. The domain of the given function f(x) is the set {10, 20, 30}.

All we can say about

`{f}^( - 1) (x)`

is that, it has a range of {10, 20, 30}.

This is because the domain of a function becomes the range of its inverse function.

2. If the graph of a function f(x) includes the point (3, 0), then the graph of the inverse function ,

`{f}^( - 1) (x)`

will contain the point (0,3).

Reason:The point on the graph of the inverse function is obtained by reflecting the corresponding point on the graph of the function in the line y=x. We just have to swap the coordinates.

In simple terms the domain of the function becomes the range of the inverse function and vice versa.

3. If the first term in an arithmetic sequence is 2.

Then we have a=2.

If the twelfth term is 211, then

`a + 11d = 211...(1)`

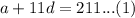
Put a=2 into this equation.

`2 + 11d = 211`

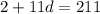
Solve for d.

`11d = 211 - 2`

`11d = 209`

`d = (209)/(11) = 19`

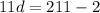
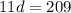
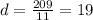
If

`a_n = 135`

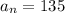
then

`a + (n - 1)d = 135`

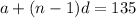
Substitute a=2 and d=19

`2 + (n - 1)19 = 135`

`19(n - 1) = 133`

`(n - 1) = (133)/(19)`

`n - 1 = 7`

`n = 7 + 1 = 8`

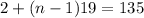
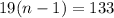
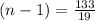
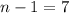
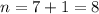
Therefore n=8